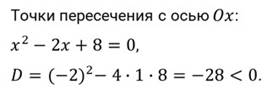- Постройте графики функций с помощью производной первого порядка
- Решение.
- Постройте графики функций с помощью производной первого порядка
- Решение
-         1) Областью определения является вся действительная ось .         2) Найдём пересечение с осями координат.         Пересечение с осью Oy :      .         Пересечение с осью Ox:      .         Отсюда     и      .         3) Функция ни четная, ни нечетная. Действительно и .         4) Найдём производную .         Производная равна нулю в точке        . Производная не существует в точках         и        .         При               производная положительная.
- Построение графика функции методом дифференциального исчисления
- Правила ввода функции
- Применение производной к построению графиков функций
- Урок 13. Алгебра 11 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Применение производной к построению графиков функций»
Постройте графики функций с помощью производной первого порядка
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
      Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
      Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
      Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29
      Вариант 30     Вариант 31
        1.3 Построить график функции с помощью производной первого порядка
Решение.
        1) Областью определения функции является вся числовая ось. То есть     
        2) Функция ни четная, ни нечетная, так как     

        3) Найдём производную функции

        4) Найдём критические точки, в которых производная обращается в ноль     
        Это точки     
        Таким образом:     



        5) Строим график на основании проделанного исследования.

Источник
Постройте графики функций с помощью производной первого порядка
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
        Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
        Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
        Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        Вариант 31
        2.1 Построить график функции с помощью производной первого порядка.
Решение
        1) Областью определения является вся действительная ось  .         2) Найдём пересечение с осями координат.
.         2) Найдём пересечение с осями координат.
        Пересечение с осью Oy :       .
 .
        Пересечение с осью Ox:       .
 .
        Отсюда      и    
    и       .         3) Функция ни четная, ни нечетная. Действительно
 .         3) Функция ни четная, ни нечетная. Действительно  и
и  .         4) Найдём производную
.         4) Найдём производную  .         Производная равна нулю в точке    
.         Производная равна нулю в точке         . Производная не существует в точках    
   . Производная не существует в точках          и    
    и         .
   .
        При                производная положительная.
      производная положительная.
        Следовательно, при       
        При     
        Следовательно, при     
        В точке     

        В точках     

        5) На основании проведённого исследования строим график. 
Источник
Построение графика функции методом дифференциального исчисления
Правила ввода функции
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пример №1 . Провести полное исследование функции 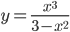
1) Функция определена всюду, кроме точек 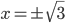
2) Функция нечетная, так как f(-x) = -f(x) , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке 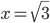
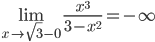
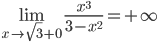
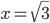
6) Находим 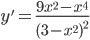
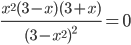
В окрестности точки x3=3 имеет: y’>0 при x 3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2. Найти первую производную функции
7) Находим 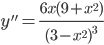

8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты 

Найдем наклонные асимптоты: 

9) Теперь, используя полученные данные, строим чертеж:

Пример №2 . Построить график функции 
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем 

4. Точки разрыва x=0 , причем 
Найдем наклонные асимптоты: 

Наклонная асимптота имеет уравнение y=x .
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем 
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Источник
Применение производной к построению графиков функций
Урок 13. Алгебра 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Применение производной к построению графиков функций»
Сегодня на уроке мы приведём общую схему исследования свойств функции с помощью её производной. Будем строить график функции, используя результаты исследования.
Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что на предыдущих занятиях мы рассмотрели применение производной к нахождению промежутков возрастания и убывания функций. Выяснили, какие точки называют точками максимума функции и точками минимума функции. Научились находить эти точки и значения функции в них. Сегодня на уроке мы применим эти знания к построению графиков функций.
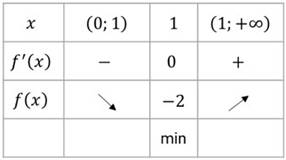
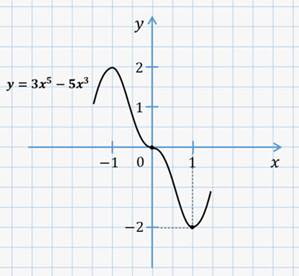
Давайте начнём с примера. Итак, постройте график функции 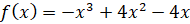
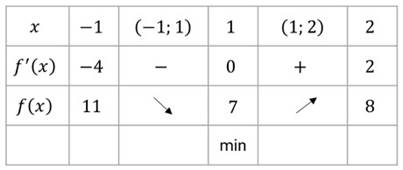
Полученные результаты исследования функции удобно записать в виде следующей таблице.
В первой строке этой таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. Во второй строке отмечены знаки производной на этих промежутках. В третьей строке записаны выводы о ходе изменения данной функции, в четвёртой строке – о виде критических точек.
При построении графика обычно находят точки пересечения графика с осями координат.
Построим график функции.
Получается, что для построения графика функции сначала исследуют свойства этой функции с помощью её производной.
Давайте приведём схему исследования свойств функции с помощью её производной.
Итак, при исследовании свойств функции надо найти:
1) область определения; производную; стационарные точки;
2) промежутки возрастания и убывания;
3) точки экстремума и значения функции в этих точках.
Результаты исследования удобно записать в виде таблицы, используя которую, строят график функции. Для более точного построения графика обычно находят точки пересечения с осями координат. Также можно найти координаты ещё нескольких точек графика.
Отметим, что для построения графика чётной (нечётной) функции достаточно исследовать свойства и построить её график при 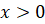
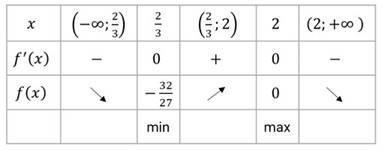
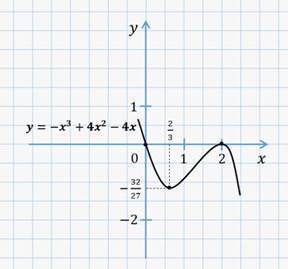
Давайте построим график функции 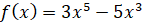
Полученные результаты исследования запишем в виде таблицы.
Найдём значение функции в точке 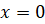
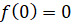
Построим график функции.
Так как рассматриваемая функция является нечётной, то её график при 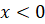
Часто встречаются задачи, в которых требуется исследовать функцию не на всей области определения, а на некотором промежутке.
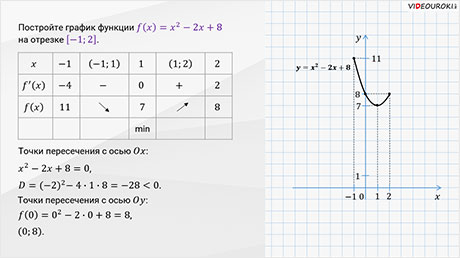
Давайте построим график функции 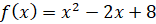
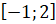
Запишем полученные результаты исследования функции в виде таблицы.
Получается, что график функции не пересекает ось абсцисс.
Источник



 .         2) Найдём пересечение с осями координат.
.         2) Найдём пересечение с осями координат.   .
 .  .
 .      и    
    и       .         3) Функция ни четная, ни нечетная. Действительно
 .         3) Функция ни четная, ни нечетная. Действительно  и
и  .         4) Найдём производную
.         4) Найдём производную  .         Производная равна нулю в точке    
.         Производная равна нулю в точке     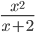 ≡ x^2/(x+2)
≡ x^2/(x+2) 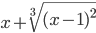 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)