Получить две первых при помощи 3 кусков

Нужно получить 2/1 при кусков.

Ответы

1)3 3/4 дм=3.75 дм
3.75:5=0.75 (дм)
а)14:4=3.5(м)

3) 7 1/2 м=750 см
750:50=15(кусков)
а) 5 1/2 кг=5500 г
5500:250=22(п.)

4) 2 1/5 л=11/5 л
11/5:1/4=44/5=8 4/5 чашки
полных чашек 8
а) 2 1/2 м=2.5 м
17:2.5=6.8 (п.)
можно перевязать 6 посылок,на седьмую не хватит
5) 2:3/10=2*10/3=20/3=6 (ост 2)-
6 полных банок и одна неполная,итого 7 банок нужно
а) 8:3/5=8*5/3=40/3=13(ост 1)-
13 полных и одна неполная ,итого 14 бутылок

6) 40 1/2=81/2 км
81/2:2/3=81/2*3/2=243/4=60.75 км/ч
а) 10 1/2=21/2 км
7:21/2=7*2/21=2/3 ч или 40 мин
б) 2 2/3 ч=160 мин
24 км-160 мин
30 км-?
160*30:24=200(мин)=3 1/3ч

9.
Пусть х — ширина прямоугольника. Тогда 3х — длина прямоугольника.
Р = 2(х+ 3х)
2(х+3х) = 24
2•4х=24
8х=24
х=24:8
х=3 см — ширина прямоугольника.
3•3=9 см — длина прямоугольника.

11.
Пусть а — длина проволоки.
1) а • 20% = 0,2а — отрезали проволоки от куска в первый раз.
2) а-0,2 = 0,8 а — остаток проволоки после первого отрезания.
3) 0,8 • 4% = 0,8а • 0,0,4 = 0,032а проволоки отрезали во второй раз.
4) 0,8а — 0,032а = 0,768а проволоки осталось.
5) 0,768 = 76,8% проволоки осталось.

21-4) получена тысяча рублей. 22-1) АБВ. 23-2) Поток воды, камней, льда обрушился в пропасть с нарастающим устремлением. 24-4) 1,2,3. 25-2) Всё в снегу: и двор, и деревья, и крыльцо.

4 Получена тысяча рублей

22 Укажите предложение, в котором ставится тире. А Сохранение природы существенная задача. 2 АВГ

23 В каком предложении нужно поставить две запятые? 2 Поток воды, камней, кусков льда обрушился в пропасть с нарастающим устремлением.

24 Укажите правильный вариант расстановки запятых в предложении. Лошади удивлялись шуму воды(1)поднимали головы(2) настораживались(3)но мерно и осторожно(4)продолжали шагать против течения. 4. 1,2,3

25 Укажите предложение, в котором ставится двоеточие. 2 Все в снегу: и двор, и деревья, и крыльцо.

Вариант № 44588
1. Найди значение выражения 81 − 32 = 49

2. Найди значение выражения 4 + 6 · (14 + 6) = 124
1) 14 + 6 = 20
2) 6 * 20 = 120
3) 4 + 120 = 124
3. У Марины есть список продуктов, которые ей нужно купить:
Масло — 1 пачка = 1 * 80 = 80 руб
Сахар — 1,5 кг = 1,5 * 46 = 69 руб
Яблоки — 2 кг = 2 *70 = 140 руб
Хлеб белый — 1 батон = 1 * 23 = 23 руб
Сколько сдачи она получит с 500 рублей, если пачка масла стоит 80 рублей, килограмм яблок — 70 рублей, батон хлеба — 23 рубля, а килограмм сахара — 46 рублей?
Запиши решение и ответ. 80 + 69 + 140 + 23 = 312 руб вся покупка
500 — 312 = 262 руб сдача
4.Для украшения зонтика от солнца потребовалась кружевная лента длиной 7 м 44 см. На сколько сантиметров надо укоротить ленту длиной 8 метров, чтобы получить ленту нужной длины?
8 м — 7 м 44 см = 800 см — 744 см = 56 см настолько укоратить
5. На опытном участке выращиваю экспериментальные сорта овощей. В таблице приведены данные о количестве овощей, собранных с июля по сентябрь.
Месяц Овощи
Огурцы Морковь Помидоры
Июль 13 9 10
Август 35 24 24
Сентябрь 49 31 49

В каком месяце было собрано одинаковое количество огурцов и помидоров? ответ: в сентябре
6. В течение трёх лет учитель фиксировал количество «пятёрок» за контрольные работы по математике для одной и той же группы детей. Эти данные представлены в таблице.
Месяц Год
2013 год 2014 год 2015 год
Сентябрь 16 14 17
Октябрь 6 4 10
Ноябрь 8 16 5
Декабрь 16 5 18

Сколько всего пятёрок было получено за 2014 год?
14 + 4 + 16 + 5 = 39
7. Найди значение выражения 963 : 3 − (753 − 468) = 36
1) 753 — 468 = 285
2) 963 : 3 = 321
3) 321 — 285 = 36
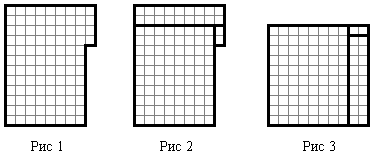
8. Стандартный прут арматуры имеет длину 11 м 70 см. Требуется разрезать его на длинные и короткие куски длиной 1 м 10 см и 70 см соответственно. При этом длинных кусков должно получиться не меньше шести. Какое наибольшее число коротких кусков может при атом получиться?
Запиши решение и ответ.
1) 11 м 70 см = 1170 см
2) 1 м 10 см = 110 см
3) 110 см * 6 = 660 см надо для длинных
4) 1170 — 660 = 510 см останется
5) 510 : 70 = 7,286 наибольшее может 7 шт получится
9. Вася, Маша, Юля и Петя собирали грибы. Вместе они собрали 82 гриба. Петя собрал 11 грибов, а Маша 23. Больше всего грибов собрала девочка. Кто-то из детей собрал 26 грибов.
Сколько грибов собрал Вася?
1) 11 + 23 + 26 = 60 собрали трое
2) 82 — 60 = 22 гриба собрал Вася
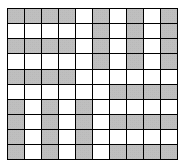
10. Бусы составлены из розовых и фиолетовых бусинок, которые идут в таком порядке: одна розовая, две фиолетовых, три розовых, четыре фиолетовых, пять розовых, шесть фиолетовых и т. д., всего 55 бусинок.
Сколько всего фиолетовых бусинок содержат эти бусы?

11. В «Детском мире» продавали двухколёсные и трёхколёсные велосипеды. Максим пересчитал все рули и все колёса. Получилось 12 рулей и 27 колёс. Сколько трёхколёсных велосипедов продавали в «Детском мире»?
Запиши решение и ответ.
2х колесные = Х
3х колесные = У

х + у = 12 х = 12 — у
2х + 3у = 27 2 * (12 — у) + 3у = 27
24 — 2у + 3у = 27
у = 27 — 24
у = 3 — это трехколесные
х + 3 = 12
х = 12 — 3
х = 9 это двухколесные
ответ: 2х колесные — 9 шт
3х колесные — 3 шт

Источник

Получить две первых при помощи 3 кусков

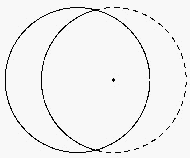
a) Нужно вырезать из круга два маленьких равных кружка — один с центром в центре круга, а другой с центром в отмеченной точке, и затем поменять эти кружки местами.

б) Линия разреза — дуга того же радиуса, что и у данного круга, с центром в отмеченной точке (см. рис.).

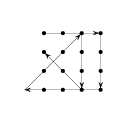
а) Проведём прямую, содержащую одну из сторон квадрата. Если точка лежит по другую сторону от этой прямой, чем квадрат, то она точно не лежит в квадрате. Иначе проведём прямую, содержащую вторую сторону квадрата и проведём аналогичные рассуждения. Проведя все четыре прямые, содержащие стороны квадрата, мы узнаем, лежит ли точка внутри квадрата.

б) Проведём сначала две прямые, содержащие диагонали квадрата. Они разобьют лист бумаги на четыре части. По ответам на первые два вопроса мы узнаем, в какой из этих частей лежит точка. Теперь проведём прямую, содержащую ту сторону квадрата, которая лежит в той же части плоскости, что и точка. Эта прямая разобьёт указанную часть плоскости ещё на две части, одна из которых будет внутри квадрата, а другая — снаружи. По ответу на третий вопрос мы узнаем, лежит ли точка внутри квадрата. Обратите внимание: теперь мы знаем не только то, лежит ли точка внутри квадрата, но и то, в какой из четырёх частей квадрата (на которые его делят диагонали) она лежит.

В этом решении ничего не сказано о случаях, когда точка оказывается на одной или нескольких из прямых, которые мы проводим. Разберите эти случаи самостоятельно.

Источник

Я оч сорри за множественные оффы. Задачка

Что-то она мне понравилась сильно.

Верёвку длиной 1 метр режут на три произвольных куска. Определить вероятность того, что хотя бы один кусок окажется длиннее полуметра.

Попробовал это сделать 10000 раз

в 7502 случаях получил >0.5

так что — похоже на 3/4

Алгоритм генерю 10тыс раз по два числа ф-цией аля random в интервале от 0 до 1. Кладу это все в таблицу БД.

а потом делаю запрос типа

select count(*)
from
(
select n01,n02,
least(n01,n02) N1, 1-greatest(n01,n02) N2, greatest(n01,n02)-least(n01,n02) n3
from
TABLE
)
where n1>0.5 or n2>0.5 or n3>0.5

хм, а разве не по этой формуле? е=е1+е2
где е вероятность события

в первом событии вероятность равна 0,5
во втором 0,5*0,5
итого вероятность равна 0,75 или 3/4 как и писали ранее?)

Вы ошибаетесь > Фиксируем на верёвке произвольный полуметровый отрезок.

Задачи «выберем две случайные точки разрезов» и «сделаем случайный разрез а затем случаноо выберем один из отрезков и случайно его разрежем» имеют разные вероятности.

Нет, не ошибаюсь Если считать по дереву событий, решение сойдётся к той же четвертушке.

К слову, я когда узнал решение, тоже не поверил и прогнал на данных random.org. На 10 тысячах попыток вышло 0,25 с погрешностью меньше полупроцента. Так что сорри, решение правильное

давайте подробнее про дерево решений конечно, у той задачи, которую вы посчиталь эквивалентной, решение 25%. А у исходной — 50%.

Итак ,первый шаг — первый рез веревки. Всего два отличных варианта — 50 см ( А ) и <>50 см — Б.

Второй шаг вслед за А — нам не важны подробности, все равно куска более 50 см нет.

Второй шаг вслед за Б — тоже всего два ответа.
С — разрезали длинный кусок
D — разрезали короткий кусок

Во-первых, первый и второй рез события независимые. Т.е. то, как резали первый раз не влияет на то, как будут резать второй. тоесть произведение вероятностей BxD, ведь нас устраивает тока D. Какова его вероятность?

тут возможно два подхода. А чем руководствовался тот, кто режет? Иными словами, пропорциональна ли вероятность длине веревки? Т.е. подходит ли модель точки, падающий на отрезок?

Я считаю, что нет. Так же, как и то, что вероятность события А=0. Вывод — B=100%, а BxD=100%xD. Поскольку с равной вероятностью разрежут как короткую, так и длинную веревку, то будет 50% в итоге.

Источник

Текстовые задачи на части, решаемые с конца

Разделы: Математика

Цели урока:

1. Обобщить и систематизировать знания и умения учащихся по теме “Нахождение целого по его части”.
2. Актуализация опорных знаний в условиях решения задачи.
3. Развитие умения решать задачи с помощью чертежа, без составления уравнений.

Ход урока

Учитель ставит цель урока и переходит к работе по теории.

1. Что такое дробь?
2. Какие виды дробей вы знаете?
3. Что показывает числитель и знаменатель обыкновенной дроби?
4. Как число умножить на дробь?
5. Как разделить число на дробь?
6. Как найти часть от числа?
7. Как найти целое, зная его часть?

Эти теоретические знания будут использованы для решения задач на уроке.

1. Мальчик прочитал книгу за 3 дня. В первый день он прочитал 0,2 всей книги и еще 16 страниц, во второй день 0,3 остатка и еще 20 страниц. В третий – 0,75 нового остатка и последние 30 страниц. Сколько страниц в книге?

Для решения необходим чертеж. Умение строить чертеж, понимать его – половина успеха в решении задач, рассматриваемого типа.

1. 30 :(1 – 0,75) = 120 (стр.) – осталось прочитать после второго дня;
2. 120 + 20 = 140 (стр.) – остаток после второго дня чтения;
3. 140 : (1 – 0,3) = 200 (стр.) – осталось прочитать после первого дня;
4. 200 + 16 = 216 (стр.) – остаток после первого дня чтения;
5. 216 : ( 1 – 0,2) = 270 (стр.) – столько страниц в книге

Ответ: 270 страниц в книге, которую читал школьник.

2. Турист совершил переход на велосипедах в три дня. В первый день они прошли всего пути без 2 км. Во второй день – половину оставшегося пути без 3 км и в третий день – оставшегося пути и еще 6 км. Сколько километров проехали туристы за три дня?

1) – второго остатка составляют 6 км;
2) (км) – проехали туристы во второй день;
3) 54 – 3 = 52 (км) – половина первого остатка;
4) 51 : 0,5 = 102 (км) – первый остаток;
5) 102 – 2 = 100 (км) –2/3 всего пути;

6) (км) – весь путь

Ответ: за три дня туристы проехали 150 км

3. База отпустила четырем столовым картофель. Первой столовой отпущено 0,125 всего картофеля и еще 10 кг, второй – остатка и еще 40 кг, третьей – 0,4 нового остатка, четвертой столовой – 0,75 третьего остатка и остальные 57 кг. Сколько картофеля отпущено всем четырем столовым?

1) 57 : ( 1 – 0,75) = 228 (кг)отпущено четвертой столовой;
2) 228 : ( 1 – 0,4) = 380 (кг) отпущено третьей и четвертой столовой вместе;
3) 380 + 40 = 420 (кг) остаток после второй столовой без 40 кг;
4) (кг) осталось отпустить после первой столовой;
5) (620+10) : (1 – 0,125) = 630: 0,875 = 720 (кг) отпущено картофеля.

Ответ: 720 кг картофеля отпущено четырем столовым.

4. Магазин продал кусок ткани в течение четырех дней. В первый день было продано всего куска и еще 5 м, во второй 20% остатка и еще 10 м, а в третий день – 25 % нового остатка и еще 9 м и в четвертый день того, что осталось после продажи в третий день, и остальные 13 м. сколько метров было в куске?

1) приходится на 13 м;
2) (м) продали в четвертый день;
3) ;
4) 19,5 + 9 = 28,5 (м) – 3/4 нового остатка;
5) (м) – новый остаток;
6) 4
7) 38 +10 = 48 (м) – 4/5 остатка;
8) (м) – остаток;
9) ;
10) 60 + 5 = 65 (м) – нового остатка;
11) (м) было ткани;

Ответ: в куске было 78 м ткани.

Не все задачи, конечно могут быть рассмотрены на одном занятии, но нам кажется, что для развития мышления учеников, к ним имеет смысл возвращаться на других уроках.

Итог урока: Учитель еще раз подчеркивает, что для того чтобы решить задачу на части нужно сделать чертеж.

Домашнее задание: по усмотрению учителя две задачи из приведенных ниже.

5. Рыбный магазин продал в первый день 0,3 всего числа полученных ими банок осетрины и 1/7 остатка; во второй день – 3/8 того, что осталось после первого дня; в третий 5/12 того, что осталось после второго дня и 1/7 нового остатка, в четвертый день – остальные 3 десятка банок. Сколько банок осетрины получено магазином?

6. Для посадки продавались черенки смородины. Первый покупатель взял 0,2 всех черенков и еще 2 черенка, второй взял1/3 оставшихся и еще 2 черенка. Третий взял 0,5 оставшихся после второго покупателя черенков смородины. Четвертый взял остальные 9 черенков. Сколько черенков смородины было продано?

7. Колхозник продал картофель трем покупателям: первому – 0,25всего и еще 10 кг, второму – 5/11 остатка и еще 10 кг, а третьему – последние 50 кг. Сколько картофеля продал колхозник?

Ответ: 160 кг картофеля продал колхозник.

8. Строительная организация получила сначала отпущенных ей денег, затем остатка и, наконец. Последние 9500 руб. За кирпич уплатили в 3 раза больше, чем за цемент, а за кровельное железо на 670 руб. больше, чем за кирпич. Какая сумма была внесена отдельно на оплату кирпича, кровельного железа и цемента?

Литература:

1. Г.И.Зубелевич Сборник задач Московских математических олимпиад. “Просвещение” М.1971.
2. С.А.Пономарев, П.В.Стратилатов, Н.И.Сырнев Сборник задач по математике для 4-5 классов “Просвещение” М.1979.

Источник