Как вычислить общий объем лекарственного вещества

Содержание

Общий объем микстуры
Определение общего объема жидкой лекарственной формы
Общий объем микстуры
Как вычислить общий объем лекарственного вещества

Общий объем микстуры

Объем жидкого лекарства определяется суммированием объемов жидких ингредиентов: растворов лекарственных веществ, галеновых, новогаленовых и других жидких препаратов.

Rp.: Kalii bromidi 5,0
Natrii bromidi 4,0
Kaiii iodidi 6,0
T-гае Valerianae 10,0
Aq. destill. 200,0
MDS . По 1 столовой ложке 3 раза в день

Общий объем микстуры слагается из объемов настойки и воды и равен 210 мл. Микстуру приготовляют с применением концентрированных растворов.

Во флакон для отпуска отмеривают из бюретки 95 мл дистиллированной воды, 25 мл 20% раствора калия бромида (1:5), 20 мл 20% раствора натрия бромида (1:5), 60 мл 10% раствора калия йодида.

После проверки жидкости на отсутствие механических примесей к водному раствору добавляют из бюретки 10 мл настойки валерианы. Затем микстуру укупоривают и оформляют для отпуска.

Необходимо учесть, что лекарство содержит светочувствительные препараты, поэтому на флакон приклеивают этикетку «Хранить в защищенном от света месте».

Rp.: Natrii hydrocarbonatis 2,0
Natrii benzoatis 4,0
Elixiris pectoralis 5,0
Sirupi simplicis 20,0
Aq. destill. 200,0
MDS . По 1 столовой ложке 3 раза в день

Общий объем микстуры — 225 мл. Объем концентрированных растворов: 5% раствора натрия гидрокарбоната (1:20) — 40 мл, 10% раствора натрия бензоата (1:10) — 40 мл. Объем дистиллированной воды: 200-(40 + 40) = 120 мл.

Во флакон для отпуска отмеривают из бюреток 120 мл дистиллированной воды, 40 мл 5% раствора натрия гидрокарбоната (1:20), 40 мл 10% раствора натрия бензоата (1:10). После проверки жидкости на отсутствие механических примесей добавляют 20 мл сахарного сиропа и 5 мл грудного эликсира. Затем флакон укупоривают и оформляют для отпуска.

Rp.: Codeini phosphatis 0,1
Natrii bromidi
Natrii hydrocarbonatis aa 5,0
T-rae Valerianae 15,0
Aq. destill. ad 200,0
MDS . По 1 столовой ложке 3 раза в день

Если количество растворителя в рецепте указано «до определенного объема», то объем жидких препаратов включается в объем водного раствора.

Общий объем микстуры — 200 мл, объем концентрированных растворов: 20% раствора натрия бромида (1:5) — 25 мл, 5% раствора натрия гидрокарбоната (1:20) — 100 мл, 1% раствора кодеина фосфата (1:100)— 10 мл. Объем дистиллированной воды: 200 — (25 -5 100 + 10 + 15) = 50 мл.

Во флакон для отпуска отмеривают из бюретки 50 мл дистиллированной воды, 10 мл 1 % раствора кодеина фосфата (1:100), 25 мл 20% раствора натрия бромида (1:5), 100 мл 5% раствора натрия гидрокарбоната (1:20), после проверки жидкости на отсутствие механических примесей добавляют 15 мл настойки валерианы. Затем флакон укупоривают и оформляют для отпуска.

«Пособие для фармацевтов аптек», Д.Н.Синев

Источник

Определение общего объема жидкой лекарственной формы

При определении общего объема жидкой лекарственной формы следует принимать во внимание способ выписывания рецепта.

1.При раздельном выписывании компонентов общий объем лекарственной формы определяют суммированием всех жидкостей, перечисленных в прописи рецепта:

Рецепт № 1. Rp.: Codeini 0,15

Natrii benzoatis ana 4,0

Liquoris Ammonii anisati 5,0

Sirupi simplicis 10,0

Aqua purificata 200,0

Signa. По 1 столовой ложке 3 раза в день

В этом случае общий объем определяется суммированием объемов всех жидких ингредиентов V_общ = 200 мл + 5 мл + 10 мл = 215 мл

2. Врач в рецепте указывает общий объем лекарственной формы:

Рецепт № 2 Rp.: Codeini 0,15

Natrii benzoatis ana 4,0

Liquoris Ammonii anisati 5,0

Sirupi simplicis 10,0

Aqua purificata ad 200,0

Signa. По 1 столовой ложке 3 раза в день

Общий объем равен 200 мл.

3. Иногда в рецептурной прописи могут быть выписаны жидкости, которые дозируются по массе. В этом случае чтобы определить общий объем

лекарственной формы необходимо весовые единицы перевести в объемные по формуле V= 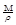, где M — масса жидкости; ρ – плотность жидкости.

Рецепт № 3. Rp.: Sol. Kalii acetatis 10% — 100 ml

Glycerini 10 ml

Глицерин выписывается в весовых единицах (приказ №308). Необходимо пересчитать, какой объем будут занимать 10 г глицерина (ρ_{глицер.} = 1,228).

V_{глицер.} = 10 мл : 1,228 = 8 мл

Следовательно, V_общ = 100 мл + 5 мл + 8 мл = 113 мл.

Источник

Общий объем микстуры

Rp.: Kalii bromidi 5,0
Natrii bromidi 4,0
Kaiii iodidi 6,0
T-гае Valerianae 10,0
Aq. destill. 200,0
MDS . По 1 столовой ложке 3 раза в день

Rp.: Natrii hydrocarbonatis 2,0
Natrii benzoatis 4,0
Elixiris pectoralis 5,0
Sirupi simplicis 20,0
Aq. destill. 200,0
MDS . По 1 столовой ложке 3 раза в день

Rp.: Codeini phosphatis 0,1
Natrii bromidi
Natrii hydrocarbonatis aa 5,0
T-rae Valerianae 15,0
Aq. destill. ad 200,0
MDS . По 1 столовой ложке 3 раза в день

«Пособие для фармацевтов аптек», Д.Н.Синев

Источник

Как вычислить общий объем лекарственного вещества

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«КАРСУНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ
ИМЕНИ В.В.ТИХОМИРОВА»

УЧЕБНОЕ МЕТОДИЧЕСКОЕ ПОСОБИЕ
для студентов
по дисциплине: «Математика»

по разделу: «Математические навыки в медицине»

Для специальностей: 31.02.01 «Лечебное дело»
34.02.01 «Сестринское дело»

Составила:
Преподаватель: Тимохина Л.Н.

р.п. Карсун – 2018-19 уч.год

1. Пояснительная записка
Учебное методическое пособие составлено в соответствии с Федеральным Государственным образовательным стандартом среднего профессионального образования по специальностям: 31.02.01 «Лечебное дело», 34.02.01 «Сестринское дело».
Учебное пособие написано в помощь студентам при изучении темы: «Математические навыки в медицине»
Содержание учебного пособия соответствует рабочей программам по математике по специальностям Лечебное дело», «Сестринское дело». На изучение темы отведено 14 обязательных аудиторных часов для специальностей «Сестринское дело» и 16 аудиторных часов по специальности «Лечебное дело».
Пособие содержит краткую теоретическую часть, примеры решения типовых задач, упражнения для самостоятельного решения, вопросы для контроля. Изложение теоретического материала сопровождается большим количеством примеров и задач. Учитывая профессиональную направленность курса математики, приведены примеры и предложены задачи по дисциплинам фармакологии, педиатрии, сестринский уход в терапии. Это способствует воспитанию у студентов уверенности в профессиональной значимости изучаемого предмета. Выполняя самостоятельно практические задания, студенты убеждаются в справедливости теоретических основ математики, а также видят практическое применение математических методов в медицине. Учебное пособие дает возможность студентам самостоятельно изучить теоретический материал, способствует выработке у студентов умений и навыков анализировать усвоенный теоретический материал, а также способствует формированию умений и навыков практического применения полученных теоретических знаний по предмету при решении прикладных задач в области медицины.
Пособие предназначено для студентов медицинских колледжей. Рекомендуется применять на теоретических и практических занятиях по
дисциплине «Математика».
По итогам изучения темы студент должен
знать:
Определение процента;
Определение процентной концентрации растворов;
Понятие пропорции, основное свойство пропорции;
Меры объема – дозы лекарственных форм;
Единицы веса;
Формулы расчета максимального и минимального артериального давления детей, прибавки массы и роста, суточной калорийности пищевого рациона детей, формулу нормы количества мочи, выделяемой за сутки;
уметь:
Решать задачи на проценты;
Рассчитывать процентную концентрацию растворов;
Получать нужную концентрацию растворов;
Рассчитывать цену деления шприца (обычного и инсулинового);
Определять шоковый индекс, кровопотерю;
Уметь рассчитывать максимальное и минимальное артериальное давление у детей, прибавку роста и массы детей;
Рассчитывать суточную калорийность пищевого рациона детей;
Определять количество мочи, выделяемой за сутки у детей по формуле;
Уметь составлять и решать пропорции;
Рассчитывать количество лекарственного вещества в 1 мл. раствора;
Рассчитывать разовую, суточную и курсовую дозу лекарственных веществ, выписанных в рецепте.

2. Области применения математических методов в медицине и биологии
Различные конкретные математические методы применяются к таким областям биологии и медицины, как таксономия, экология, теория эпидемий, генетика, медицинская диагностика и организация медицинской службы. В том числе математические методы классификации применяются к задачам биологической систематики и медицинской диагностики, а также используются для исследования операций в организационных вопросах, связанных с медицинским обслуживанием.
Существенно, важен вопрос в том, в каких областях применимы математические методы. Потребность в математическом описании появляется при любой попытке вести обсуждение в точных понятиях и что это касается даже таких сложных областей как искусство и этика. Рассмотрим несколько конкретнее области применения математики в биологии и медицине.
До сих пор мы имели в виду главным образом те медицинские исследования, которые требуют более высокого уровня абстракции, чем физика и химия, но тесно связана с ними. Далее мы перейдем к проблемам, связанным с психологией человека, т.е. к использованию прикладных наук для достижения некоторых более общих целей. Эту область довольно расплывчато называют исследованием операций. Пока лишь отметим, пойдет о применении научных методов при решении административных и организационных задач, особенно тех, которые непосредственно или косвенно связаны с медициной.
В медицине часто возникают сложные проблемы, связанные с применением лекарственных препаратов, которые еще находятся на стадии испытания. Морально врач обязан предложить своему больному наилучший из существующих препаратов, но фактически он не может сделать выбор, пока испытание не будет закончено. В этих случаях применение правильно спланированных последовательностей статистических испытаний позволяет сократить время, требуемое для получения окончательных результатов.
Этические проблемы при этом не снимаются, однако такой математический подход несколько облегчает их решение.
Простейшее исследование повторяющихся эпидемий вероятностными методами показывает, что такого рода математическое описание позволяет в общих чертах объяснить важное свойство таких эпидемий – периодическое возникновение вспышек примерно одинаковой интенсивности, тогда как детерминистская модель дает ряд затухающих колебаний, что не согласуется с наблюдаемыми явлениями. При желании разработать более детальные, реалистические модели мутаций у бактерий или повторяющихся эпидемий эта информация, полученная с помощью предварительных упрощенных моделей, будет иметь очень большую ценность. В конечном счете, успех всего направления научных исследований определяется возможностями моделей, построенных для объяснения и предсказания реальных наблюдений.
Одно из больших преимуществ, правильно построенной математической модели состоит в том, что она дает довольно точное описание структуры исследуемого процесса. С одной стороны это позволяет осуществить ее практическую проверку с помощью соответствующих физических, химических или биологических экспериментов. С другой стороны. С другой стороны, математический анализ образом, с самого начала предусматривает соответствующую статистическую обработку данных.
Разумеется, множество глубоких медицинских и биологических исследований было бы успешно выполнено без особого внимания к статистическим тонкостям. Но во многих случаях планирование эксперимента, предусматривающее достаточное использование статистики, значительно повышает эффективность работы и обеспечивает получение большого объема информации о большем числе факторов при меньшем числе наблюдений. В противном случае эксперимент может оказаться неэффективным и неэкономичным и даже привести к неверным выводам. В этих случаях новые гипотезы, построенные на таких необоснованных выводах, не смогут выдержать проверку временем.
Отсутствием статистического подхода в медицине можно в какой-то мере объяснить периодическое появление «модных» препаратов или методов лечения. Очень часто врачи выбирают те или иные новые препараты или методы лечения и начинают их широко применять только на основании кажущихся благоприятных результатов, полученных на небольших выборках данных и обусловленных чисто случайными колебаниями. По мере того как у медицинского персонала накапливается опыт применения этих препаратов или методов в больших масштабах, выясняется, что возлагающиеся на них надежды не оправдываются. Однако для такой проверки требуется очень много времени, и она весьма ненадежна и неэкономична; в большинстве случаев этого можно избежать путем правильно спланированных испытаний на начальном этапе. В связи с этим, в настоящее время специалисты в области биоматематики настоятельно рекомендуют применять различные методы математической статистики при проверке гипотез, оценке параметров, планировании экспериментов и обследований, принятии решений или изучении работы сложных систем.

3. Понятие пропорций. Основное свойство пропорции.
1.1 Отношением числа a к числу b называется частное от деления числа a на число b. Записывают a/b или a : b. Например, отношение 2 к 5 равно 2/5 .
Отношение a/b показывает во сколько раз число a больше числа b, если a> b или какую часть числа b составляет число a, если a Опубликовано в Учебно-методические материалы

Источник