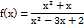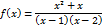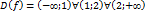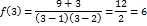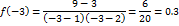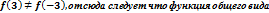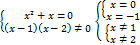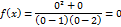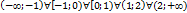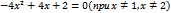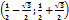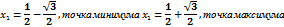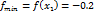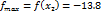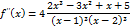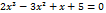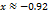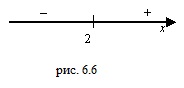Исследование монотонности функции с помощью первой производной

Исследование функции на монотонность с помощью производной.

2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x) 0, x₂>x₁

2. если f`(a) 0, то f`(x)>0

Достаточный признак: если f«(x) всюду в интервале “-”, то линия в интервале выпуклая; если f«(x)>0, то линия вогнутая

Признаки точки перегиба: чтобы X₀ была т. перегиба, чтобы у« в этой точке = 0 и меняла знак при переходе х через х₀.

Схема исследования функции. Показать на примере.

Найти:
-обл. определения ф-ции

-точки разрыва и интервалы, где ф-ция явл-ся непрерывной

-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты

-т. пересечения графика с осями координат

-симметрия графика (чет./нечет):

f(-x)=x симметрична относительно осей

f(-x)=-x симметрична относительно О(0,0)

-наибольшее и наименьшее значение

-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты

-нанесение на график.

Пример 1

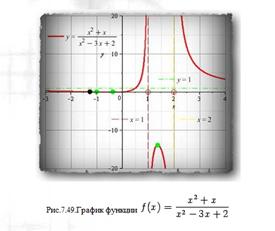
Исследовать и построить график функции

1). Заметим, что знаменатель имеет корни 1 и2, так что функцию можно представить в виде

Т.к. 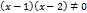, отсюда следует, что области определения функции

2)Определим тип функции, т.е. четная,нечетная или общего вида функция.

3) ,следовательно x=1 и x=2 является точкой разрыва II рода, что в свою очередь

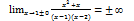
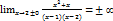
Даёт нам две вертикальные ассимптоты.

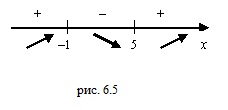
Пользуясь методом интервалов (известным из школьной программы), определим знак функции на интервалах между корнями и точками разрыва. Таких интервалов получается пять:

На этом рисунке знаком + отмечены те интервалы, на которых функция положительна, и знаком — те, где она отрицательна.

5) Найдём производную:

Решением квадратного неравенства служит интервал

6) Найдём вторую производную:

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Источник

Исследование монотонности функции с помощью первой производной

Исследование функции с помощью производной

Теоремы о дифференцируемых функциях

Теорема Лагранжа : 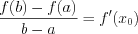, где .

Геометрический смысл теоремы: касательная к графику функции в точке параллельна секущей, соединяющей концы графика этой функции.

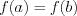
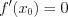
Теорема Ролля : если и , то .

Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.

Теорема Коши : если , то .

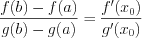
Исследование функции с помощью первой производной

С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.

Достаточное условие возрастания (убывания) функции:

а) если на заданном промежутке 0″ alt=»LaTeX formula: f'(x)> 0″ src=»http://helpy.quali.me/uploads/formulas/99b99dc08a0306fa22377c72319463ed8674d006.1.1.png»> , то функция возрастает на этом промежутке;

б) если , то функция убывает на этом промежутке.

Максимумом (минимумом) функции называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.

Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4 ).

Максимум и минимум функции называются экстремумом функции . Значение аргумента, при котором достигается экстремум, называется точкой экстремума . На рисунке 6.4 значения , , , и являются точками экстремума рассматриваемой функции.

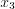
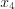
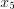
Алгоритм нахождения точек экстремума функции :

1) находим область определения функции ;
2) находим ;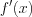

3) находим критические точки функции, решая уравнение ;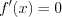

4) наносим критические точки на область определения функции;

5) определяем знак производной функции на полученных промежутках;

6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.

Рассмотрим функцию на отрезке . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.

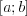
Алгоритм нахождения наибольшего и наименьшего значений функции на заданном отрезке:

1) находим ;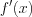

2) находим критические точки функции, решая уравнение ;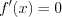

3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;

4) определяем наибольшее и наименьшее значение из полученных.

Исследование функции с помощью второй производной

Критическими точками второго рода функции называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.

Критические точки второго рода функции находят, решая уравнение .

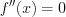
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба графика функции.

Если на некотором промежутке выполняется неравенство 0″ alt=»LaTeX formula: f»(x)> 0″ src=»http://helpy.quali.me/uploads/formulas/248b05e205897b7484fb3d48d3e089c786cb632f.1.1.png»> , то функция вогнута на этом промежутке, а если , то функция выпукла на этом промежутке.

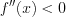
Ответ : , .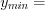

Приведем схему полного исследования функции .
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.

Источник