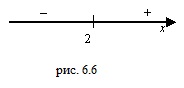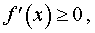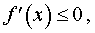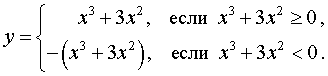- Исследование функции экстремум помощью первой производной
- Исследование функции с помощью производной
- Исследование поведения функций с помощью производной
- Интервалы возрастания и убывания функции
- Экстремумы (максимумы и минимумы) функции
- «Подозрительные» на наличие экстремума точки функции. Теорема Ферма
- Достаточные условия для существования экстремума функции
- Пример исследования поведения функции
Исследование функции экстремум помощью первой производной
Исследование функции с помощью производной
Теоремы о дифференцируемых функциях
Теорема Лагранжа : 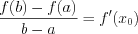

Геометрический смысл теоремы: касательная к графику функции в точке 
Теорема Ролля : если 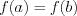

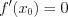
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
Теорема Коши : если 
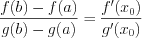
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке 0″ alt=»LaTeX formula: f'(x)> 0″ src=»http://helpy.quali.me/uploads/formulas/99b99dc08a0306fa22377c72319463ed8674d006.1.1.png»> , то функция возрастает на этом промежутке;
б) если 
Максимумом (минимумом) функции 
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4 ).
Максимум и минимум функции называются экстремумом функции . Значение аргумента, при котором достигается экстремум, называется точкой экстремума . На рисунке 6.4 значения 

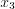
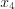
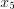
Алгоритм нахождения точек экстремума функции :
1) находим область определения функции 
2) находим 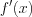
3) находим критические точки функции, решая уравнение 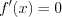
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Рассмотрим функцию 
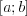
Алгоритм нахождения наибольшего и наименьшего значений функции 
1) находим 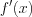
2) находим критические точки функции, решая уравнение 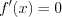
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование функции с помощью второй производной
Критическими точками второго рода функции 
Критические точки второго рода функции 
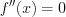
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба графика функции.
Если на некотором промежутке выполняется неравенство 0″ alt=»LaTeX formula: f»(x)> 0″ src=»http://helpy.quali.me/uploads/formulas/248b05e205897b7484fb3d48d3e089c786cb632f.1.1.png»> , то функция 
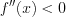
Ответ : 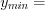


Приведем схему полного исследования функции 
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.
Источник
Исследование поведения функций с помощью производной
 Интервалы возрастания и убывания функции Интервалы возрастания и убывания функции |
 Достаточные условия для возрастания и убывания функции Достаточные условия для возрастания и убывания функции |
 Экстремумы (максимумы и минимумы) функции Экстремумы (максимумы и минимумы) функции |
 «Подозрительные» на наличие экстремума точки функции. Теорема Ферма «Подозрительные» на наличие экстремума точки функции. Теорема Ферма |
 Достаточные условия для существования экстремума функции Достаточные условия для существования экстремума функции |
 Пример исследования поведения функции Пример исследования поведения функции |
Интервалы возрастания и убывания функции
Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.
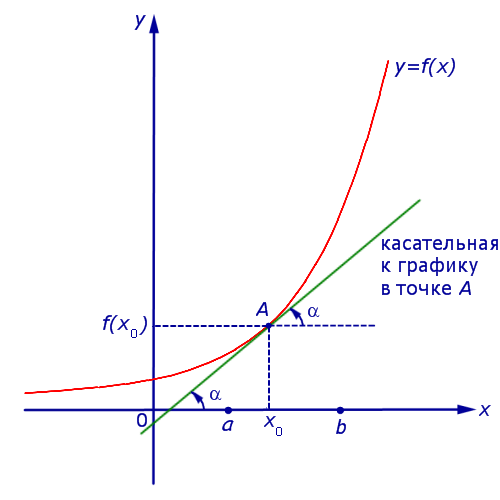
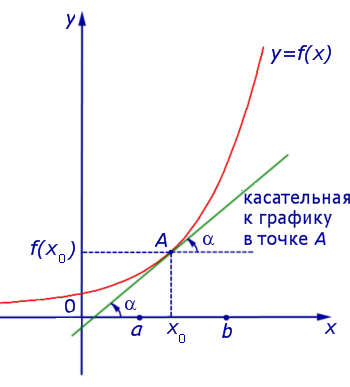
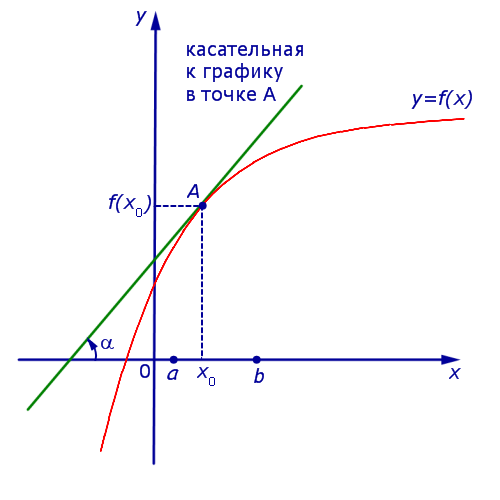
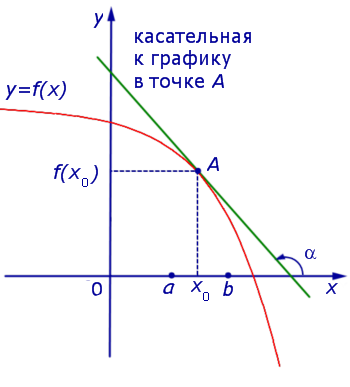
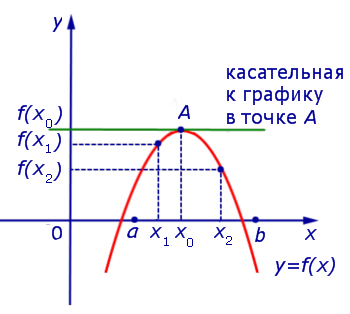
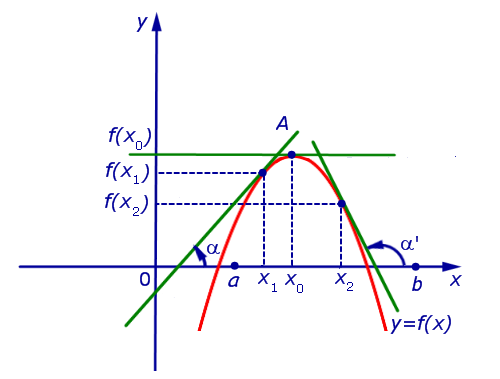
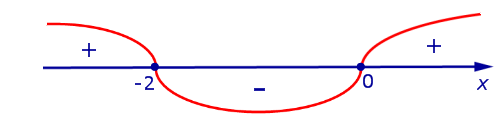
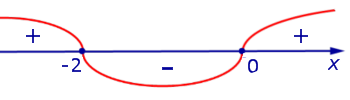
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x0 интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,
угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:
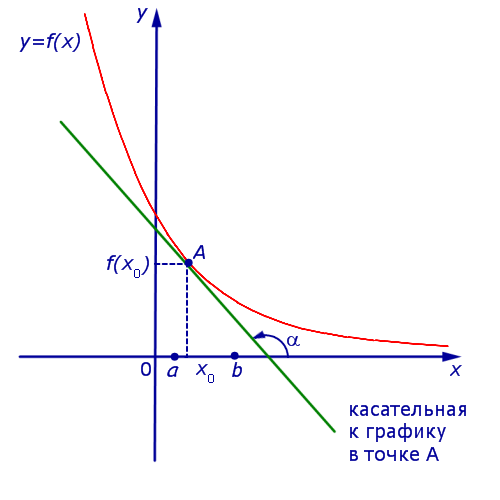
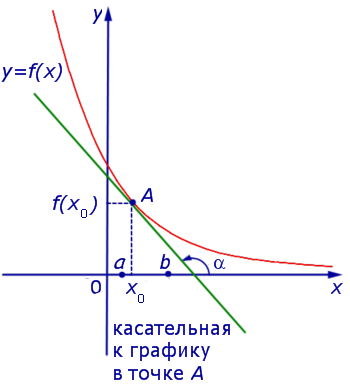
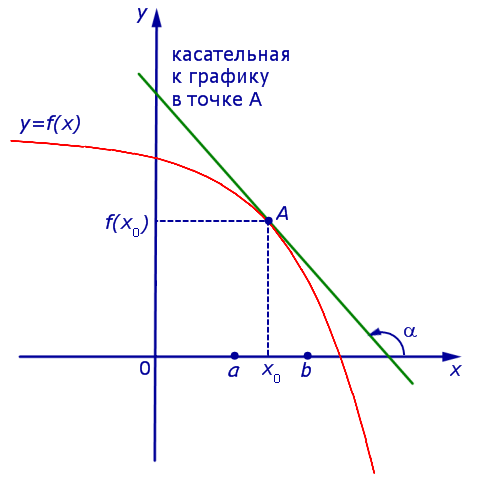
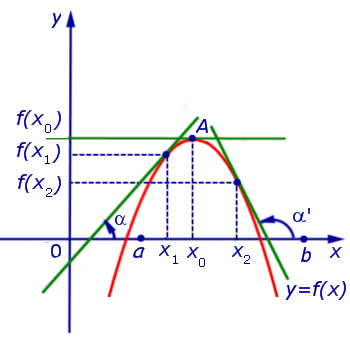
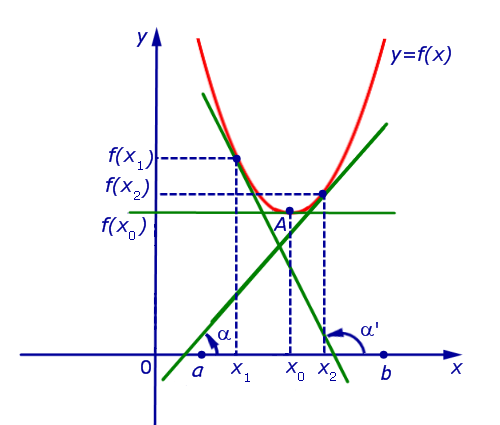
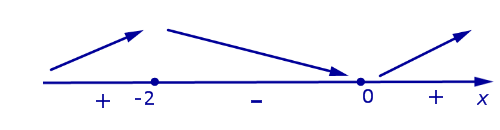
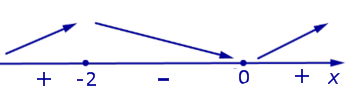
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x0 интервала имеет производную, то, как показано на рисунках 3 и 4,
угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:
а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству
Экстремумы (максимумы и минимумы) функции
Определение 1. Точку x0 называют точкой максимума функции f (x) , если существует интервал (a, b) , такой, что a для точек x которого выполнено неравенство
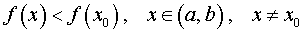
Таким образом, если x0 – точка максимума функции f (x) , то в интервале (a, b) значение функции f (x0) больше всех остальных значений функции.
Определение 2. Точку x0 называют точкой минимума функции f (x) , если существует интервал (a, b) , такой, что a для точек x которого выполнено неравенство
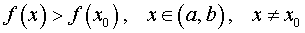
Другими словами, если x0 – точка минимума функции f (x) , то в интервале (a, b) значение функции f (x0) меньше всех остальных значений функции.
Определение 3. Точки максимума и минимума функции называют точками экстремума функции, а значения функции в точках экстремума называют экстремумами функции .
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма
Определение 4. Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.
Определение 5. Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.
Таким образом, если точка x0 является критической точкой функции, то точка x0 либо является стационарной точкой функции, либо производная функции в точке x0 не существует.
Доказательство. Если в точке x0 у функции y = f (x) не существует производная, то точка x0 является критической точкой по определению. Докажем, что если в точке x0 у функции y = f (x) существует производная, то точка x0 является стационарной, то есть f ‘ (x0) = 0 .
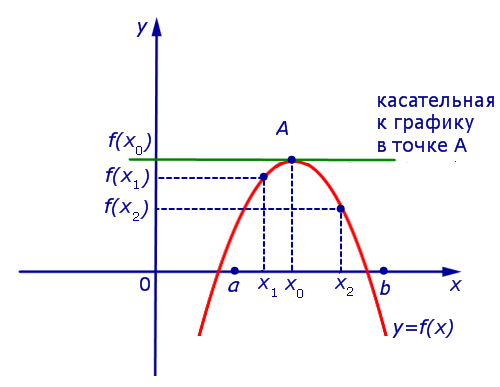
Поскольку x0 – точка максимума, то для любой точки x1 такой, что x1 , выполнено неравенство f (x1) , поэтому
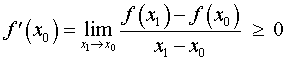
Точно так же, для любой точки x2 такой, что x2 > x0 , выполнено неравенство f (x2) , поэтому
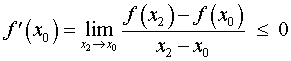
Таким образом, в случае, когда точка x0 является точкой максимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 . Касательная к графику функции y = f (x) в точке A= (x0; f (x0)) параллельна оси Ox .
Совершенно аналогично доказывается, что и в случае, когда точка x0 является точкой минимума функции y = f (x), выполнено равенство f ‘ (x0) = 0 .
Замечание 1. Из утверждения 2 следует, что точки экстремумов функции (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум .
Достаточные условия для существования экстремума функции
В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.
Утверждение 3. Рассмотрим функцию f (x) , непрерывную в интервале (a, b), содержащем точку x0 , производная которой существует в каждой точке этого интервала, кроме, быть может, самой точки x0 .
а). Если для точек 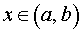
б). Если для точек 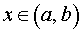
Замечание 2. Условия а) и б) утверждения 3 часто формулируют так: «Если при переходе через точку x0 производная функции меняет знак с «+» на «–» , то точка x0 является точкой максимума функции. Если при переходе через точку x0 производная функции меняет знак с «–» на «+» , то точка x0 является точкой минимума функции».
Пример исследования поведения функции
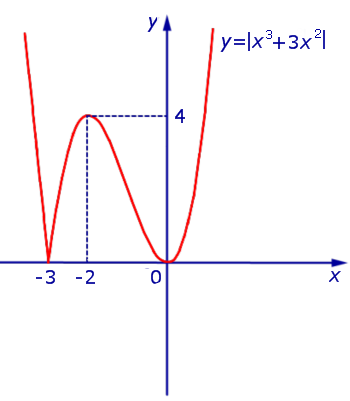
Пример. Найти интервалы возрастания, убывания и экстремумы функции
| y = | x 3 + 3x 2 | | (1) |
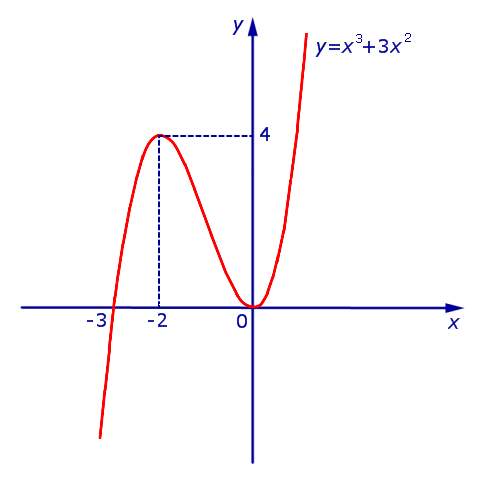
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию
| y1 = x 3 + 3x 2 | (2) |
и построим ее график. Для этого представим формулу (2) в виде
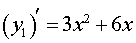 | (3) |
и разложим на множители правую часть формулы (3):
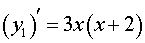 | (4) |
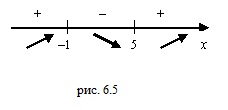
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)
Поскольку решением неравенства
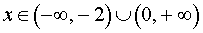 , , | (5) |
то в соответствии с утверждением 1 функция y1 возрастает на каждом из интервалов 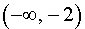
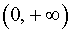
С другой стороны, поскольку решением неравенства
3x (x + 2) (– 2, 0),
то в соответствии с утверждением 1 функция y1 убывает на интервале (– 2, 0) .
Так как решениями уравнения
| x = – 2; x = 0; | (7) |
Поскольку при переходе через точку x = – 2 производная функции y1 меняет знак с «+» на «–» (рис. 8), то в соответствии с утверждением 3 точка x = – 2 является точкой максимума функции y1 , при этом
При переходе через точку x = 0 производная функции y1 меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с утверждением 3 точка x = 0 является точкой минимума функции y1 , при этом
Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).
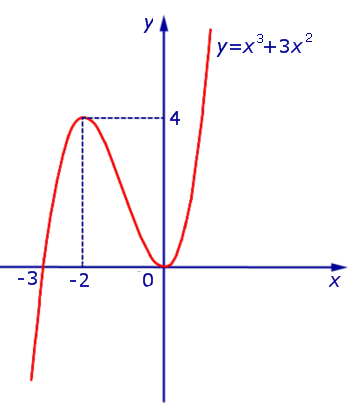
В силу определения модуля, справедливо равенство
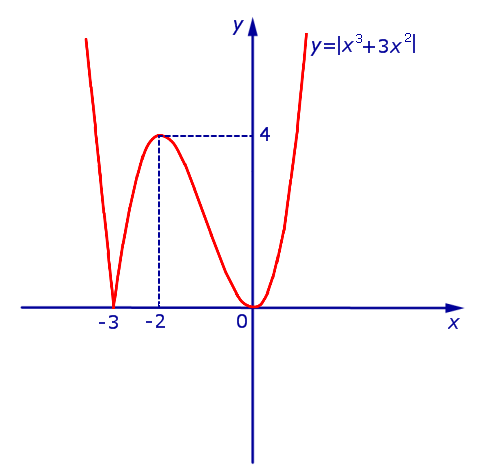
Из этого равенства вытекает, что, если мы симметрично отразим относительно оси Ox часть графика функции y1 = x 3 + 3x 2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x 3 + 3x 2 | (рис.11) .
В точке x = – 3 производная функции y = | x 3 + 3x 2 | не существует. Во всех остальных точках числовой оси производная функции y = | x 3 + 3x 2 | существует.
Точка x = – 2 является точкой максимума, причем y ( – 2) = 4 .
Функция y = | x 3 + 3x 2 | возрастает на каждом из интервалов (– 3, – 2) и 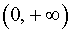
Функция y = | x 3 + 3x 2 | убывает на каждом из интервалов 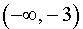
Источник