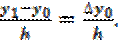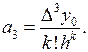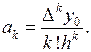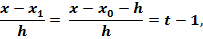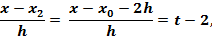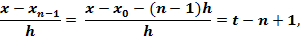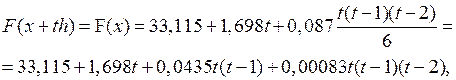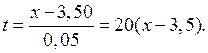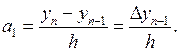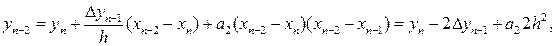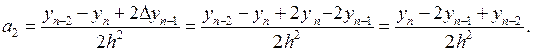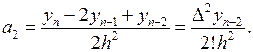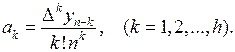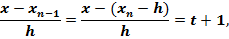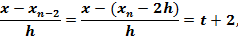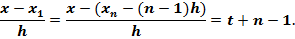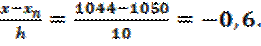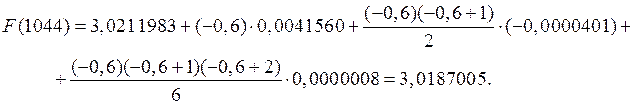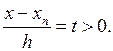Интерполяционные формулы Ньютона
При получении интерполяционных формул Ньютона, которые используются для тех же целей, что и формула Лагранжа, сделаем дополнительное предположение, что рассматриваются равноотстоящие значения аргумента. Итак, пусть значения функции у = f(x) заданы для равноотстоящих значений x0, x1 = x0 + h, …, xn = x0 + nh. Этим значениям аргументов будут соответствоватьзначенияфункции: у0 = f(x0),у1 = f(x1), …, yn = f(xn).
Запишем искомый многочлен в виде
a1 = 
Продолжая вычисления коэффициентов, положим х = х2. Тогда
y2 = y0 + 
2h + a22hh, y2 – 2Δy0 = a22h 2 ;
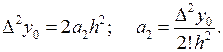
Точно так же получим 
Аналогичные дальнейшие вычисления позволяют записать общую формулу для любого коэффициента аk:
Подставим найденные выражения коэффициентов в формулу (3.9), получим
(3.10)
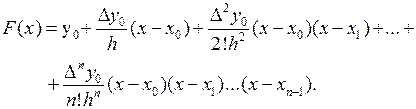
Полученная формула и называется первой интерполяционной формулой Ньютона.
Для практического использования формулу Ньютона (3.10) обычно записывают в преобразованном виде. Для этого введем обозначение
отсюда х = х0 + ht.
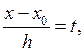
Выразим через t множители, входящие в формулу (3.10):
Подставив полученные выражения в формулу (3.10), окончательно получаем
(3.11)
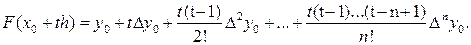
Выражение (3.11) представляет окончательный вид первой интерполяционной формулы Ньютона.
Пример. Приняв шаг h =0,05,построить на отрезке [3,5; 3,7] интерполяционный полином Ньютона для функции y = e x ,заданной табл. 3.3.
| x | 3,50 | 3,55 | 3,60 | 3,65 | 3,70 |
| y | 33,115 | 34,813 | 36,598 | 38,475 | 40,447 |
Решение. Составим таблицу разностей
| х | y | Δy | Δ 2 y | Δ 3 y |
| 3,50 3,55 3,60 3,65 3,70 | 33,115 34,813 36,598 38,475 40,447 |
Заметим, что в столбцах разностей, следуя обычной практике, мы не отделяем запятой десятичные разряды, которые ясны из столбца значений функций.
Так как разности третьего порядка практически постоянны, то в формуле (3.11) полагаем n = 3.Приняв х0 = 3,50и у0 = 33,115,будем иметь:
где 
Первая интерполяционная формула Ньютона неудобна для интерполирования функции в конце таблицы, где число значений разностей мало. В этом случае применяется вторая интерполяционная формула Ньютона, которую мы сейчас и рассмотрим.
Напишем искомый интерполяционный многочлен в виде
(3.12)
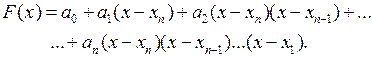
Как и ранее, коэффициенты а0,а1,…аnопределяются из условия F(xi) = yi.Положим в (3.12) х = хn.Тогда a0 = yn.
Далее, полагая в (3.12) x = xn-2и, заменяя найденные коэффициенты а0, а1их значениями, получаем
Числитель последнего выражения можно представить так:
Продолжая аналогичные вычисления, получим общую формулу для коэффициентов
После подстановки в (3.12) всех значений коэффициентов эта формула примет вид
(3.13)
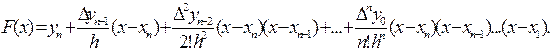
Это и есть вторая интерполяционная формула Ньютона. Для удобства применения ее, как и первую, преобразуют, введя обозначения
= tили x=xn +th.
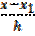
Выразим теперь через t множители в формуле (3.13):
Произведя такую замену, окончательно получим:
(3.14)
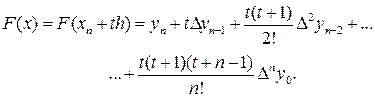
Пример. По табл. 3.5 значений семизначных логарифмов для чисел от 1000 с шагом 10 найти lg 1044.
| x | y | Δy | Δ 2 y | Δ 3 y |
| 3,0000000 3,0043214 3,0086002 3,0128372 3,0170333 3,0211893 | -426 -418 -409 -401 |
Примем xn =1050,yn =3,0211893;Δyn-1 =0,0041560;
Δ 2 yn-2 = —0,0000401;Δ 3 yn-3=0,0000008.Тогда для x=1044 получаем
t = 
Как первая, так и вторая интерполяционные формул Ньютона могут быть использованы для экстраполирования функций, т. е. для нахождения значений функций для значений аргументов х, лежащих вне пределов таблицы. Еслизначение x x0 и x близко кхп, то удобнее пользоваться второй интерполяционной формулой Ньютона, причем
Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот, – используется для интерполирования назад и экстраполирования вперед.
Пример. Имея табл. 3.6 значений и разностей,у=sin х: в пределах отх=15° дох = 55° с шагом h =5°, найти sin 14° и sin 56°.
| x( 0 C) | y | Δy | Δ 2 y | Δ 3 y |
| 0,2588 0,3420 0,4226 0,5000 0,5736 0,6428 0,7071 0,7660 0,8192 | 832 532 | -26 -32 -38 -44 -49 -54 -57 | -6 -6 -6 -5 -5 -3 |
Решение. Для вычисления sin14 0 примем x0 =15 0 и x=14 0 ,отсюда t =(14–15)/5 = – 0,2.
Здесь следует выполнить экстраполирование назад, поэтому применим первую интерполяционную формулу Ньютона и подчеркнутые одной чертой конечные разности:
sin14 0 =0,2588 + (– 0,2)0,0832+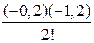 
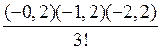
(– 0,0026) +
+ 
(–0,0006) =0,242.
Для отыскания sin56 0 примем xn =55 0 и x=56 0 ,отсюда t=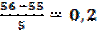 
.
Применяя вторую интерполяционную формулу Ньютона (3.14) и, используя дважды подчеркнутые разности, будем иметь:
sin56 0 =0,8192+0,2·0,0532+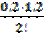 
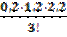
(—0,0057)+ 
(—0,0003)=0,83.
Источник
Интерполяционный многочлен в форме Ньютона
Интерполяционный многочлен в форме Ньютона
Выборка экспериментальных данных представляет собой массив данных, который характеризует процесс изменения измеряемого сигнала в течение заданного времени (либо относительно другой переменной). Для выполнения теоретического анализа измеряемого сигнала необходимо найти аппроксимирующую функцию, которая свяжет дискретный набор экспериментальных данных с непрерывной функцией — интерполяционным полиномом n -степени. Данный интерполяционный полином n-степени может быть записан, например, в форме Ньютона (один из способов представления).
Интерполяционный многочлен в форме Ньютона – это математическая функция позволяющая записать полином n -степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки с постоянным/переменным временным шагом измерений.
1. Интерполяционная формула Ньютона для неравноотстоящих значений аргумента
В общем виде интерполяционный многочлен в форме Ньютона записывается в следующем виде:
где n – вещественное число, которое указывает степень полинома;
– переменная, которая представляет собой разделенную разность k-го порядка, которая вычисляется по следующей формуле:
Разделённая разность является симметричной функцией своих аргументов, то есть при любой их перестановке её значение не меняется. Следует отметить, что для разделённой разности k-го порядка справедлива следующая формула:
В качестве примера, рассмотрим построение полинома в форме Ньютона по представленной выборке данных, которая состоит из трех заданных точек 
. Интерполяционный многочлен в форме Ньютона, который проходит через три заданных точки, будет записываться в следующем виде:
• Разделенная разность 1-го порядка определяется следующим выражением
Следует отметить, что данное выражение может быть переписано в другом виде:
• Разделенная разность 2-го порядка определяется следующим выражением
Следует отметить, что данное выражение может быть переписано в другом виде:
Форма Ньютона является удобной формой представления интерполяционного полинома n-степени, так как при добавлении дополнительного узла все вычисленные ранее слагаемые остаются без изменения, а к выражению добавляется только одно новое слагаемое. Следует отметить, что интерполяционный полином в форме Ньютона только по форме отличается от интерполяционного полинома в форме Лагранжа, представляя собой на заданной сетке один и тот же интерполяционный полином.
Следует отметить, что полином в форме Ньютона может быть представлен в более компактном виде (по схеме Горнера), которая получается путем последовательного вынесения за скобки множителей 
2. Интерполяционная формула Ньютона для равноотстоящих значений аргумента
В случае если значения функции заданы для равноотстоящих значений аргумента, которые имеют постоянный шаг измерений 
, то используют другую форму записи интерполяционного многочлена по формуле Ньютона.
• Для интерполирования функции в конце рассматриваемого интервала (интерполирование назад и экстраполирование вперед) используют интерполяционный полином в форме Ньютона в следующей записи:
где конечные разности k -порядка определяются по следующему выражению
Получаемые конечные разности удобно представлять в табличной форме записи, в виде горизонтальной таблице конечных разностей. В этой формуле из таблицы конечных разностей используются 
верхней диагонали.
• Для интерполирования функции в начале рассматриваемого интервала (интерполирование вперед и экстраполирование назад) используют интерполяционный полином в форме Ньютона в следующей записи:
где конечные разности k -порядка определяются по следующему выражению
Получаемые конечные разности удобно представлять в табличной форме записи, в виде горизонтальной таблице конечных разностей. В формуле из таблицы конечных разностей используются 
нижней диагонали.
3. Погрешность интерполяционного полинома в форме Ньютона
Рассмотрим функцию f ( x ), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином P (x) в форме Ньютона принимает в точках 
заданные значения функции 
. В остальных точках интерполяционный полином P (x) отличается от значения функции f ( x ) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Ньютона:
Абсолютную погрешность интерполяционной формулы Ньютона определяют следующим образом:
Переменная 
представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b]
В случае равноотстоящих узлов 
абсолютная погрешность интерполяционной формулы Ньютона определяют следующим образом:
Выражение записано с учетом следующей формулы:
Выбор узлов интерполяции
С помощью корректного выбора узлов можно минимизировать значение 
в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:
В качестве узлов следует взять корни этого многочлена, то есть точки:
4. Методика вычисления полинома в форме Ньютона (прямой способ)
Алгоритм вычисления полинома в форме Ньютона позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:
1. В качестве исходных данных задается выборка из n -точек, которая включает в себя значения функции и значения аргумента функции.
2. Выполняется вычисление разделенных разностей n-порядка, которые будет использоваться для построения полинома в форме Ньютона.
3. Выполняется вычисление полинома n-степени в форме Ньютона по следующей формуле:
Алгоритм вычисления полинома в форме Ньютона 
представлен на рисунке 1.
Рис.1 . Методика вычисления полинома в форме Ньютона
Следует отметить, что разделённые разности k-го порядка в соответствии с представленной методикой перезаписывается в вектор столбец функции 
, а результирующая разделенная разность всегда находится в первой ячейке функций 
. Рассмотрим, каким образом будет изменяться вектор столбец функции при выполнении расчета по представленной методике.
В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция 
на интервале [0, 10]. Необходимо построить многочлен в форме Ньютона для представленного набора значений. С помощью интерполяционной формулы вычислить приближенное значение функции в точке 
, а также определить оценку погрешности результата вычислений.
Многочлен в форме Ньютона, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Ньютона показан в графическом виде.
Рис.2 . Исходная функция и полином в форме Ньютона, построенный по шести заданным точкам
С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Ньютона в точке x =9,5 принимает следующее значение: L (9,5)= – 4,121. Из графика видно, что полученное значение не совпадает c о значением функции f ( x ) на величину абсолютной погрешности интерполяционной формулы Ньютона.
Интерполяционный полином в форме Ньютона часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Ньютона используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Источник
